数学基础
梯度
在数学中,笛卡尔坐标系下的抛物面长这样子(它的胖瘦可以任意收缩):
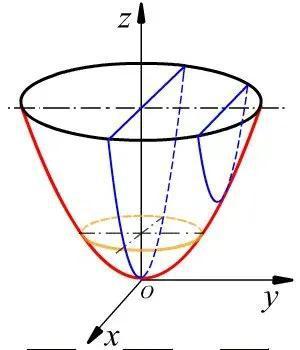
既然抛物面已经放进了数学坐标系里,那么我们能用数字符号描述它,你知道它的数学表达式是什么吗?
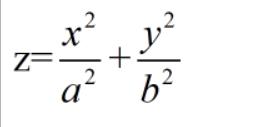
用这个公式可以描述所有的抛物面(包括卫星锅,近视眼镜片),a和b是任意常数。
梯度,我们用符号grad(f)来表示,grad是gradient的缩写,f是函数表达式的概括,具体问题具体分析。
抛物面的梯度grad是什么呢?
算抛物面梯度的公式,它长这样子:
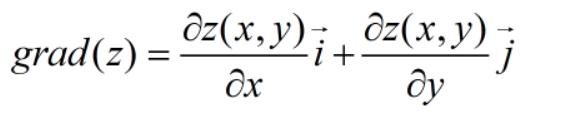
把抛物面公式带进去,你就能得到:
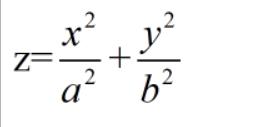
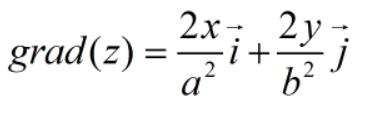
x的导数是2x,y的导数是2y
式中i 和 j 分别 是 x轴 和 y轴 的基向量,它代表的矢量为单位1。
这个表达式什么意义呢?它告诉我们,
在x轴方向上,抛物面是按照这个公式进行变化的:
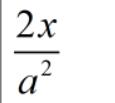
在y轴方向上,抛物面是按照这个公式进行变化的:
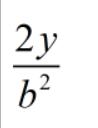
现在,让我们稍微专业一些:
我们引入梯度的定义:

二维梯度的定义

三维梯度的定义,只是增加了k方向
再引入方向导数的概念,它的意义是:指定一个你要研究的方向,在你要研究的这个方向上梯度grad是如何变化的。
你要研究的曲面部位可以用这个e向量来指向。
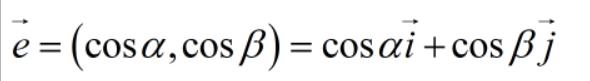
请大家仔细研究这张图:
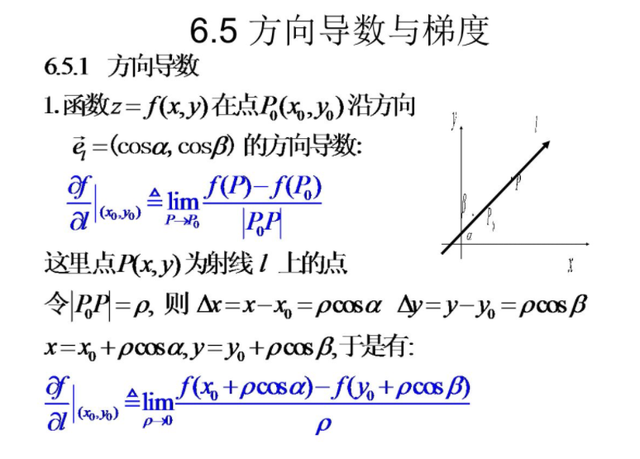
直观的梯度:
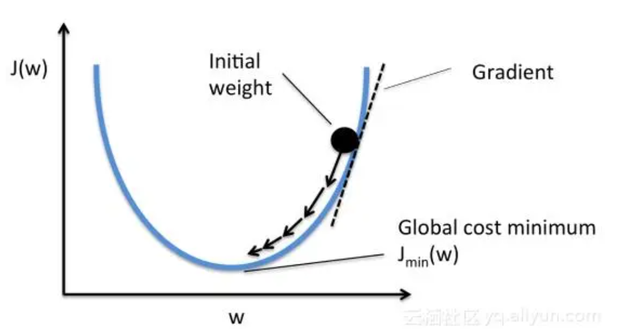
小球在抛物碗上方下落,箭头反应的就是它的梯度变化
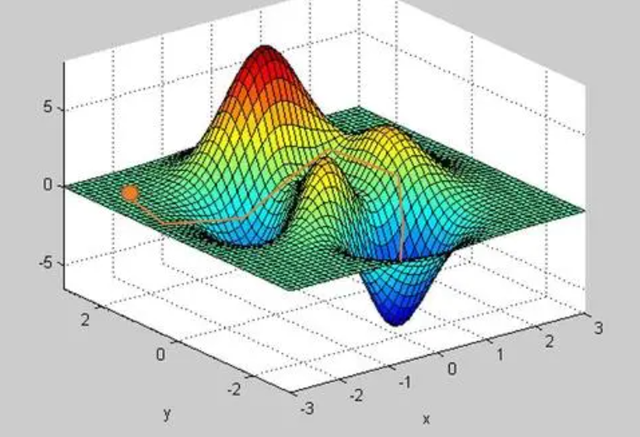
通过MATLAB得到的梯度直观变化图:图中有x,y,z三个方向,
链式法则
示例说明: 我们先以简单的复合函数为例来说明这个过程。
